A linear-time parameterized algorithm for computing the width of a DAG
Aug 1, 2021·
 ,
,
,
,
·
0 min read
,
,
,
,
·
0 min read
Manuel Cáceres
Massimo Cairo
Brendan Mumey
Romeo Rizzi
Alexandru I. Tomescu
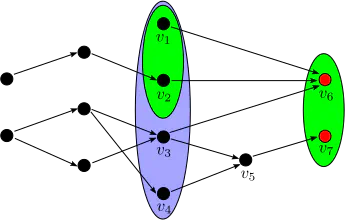 Frontier Antichains
Frontier Antichains
Abstract
The width $k$ of a directed acyclic graph (DAG) $G = (V, E)$ equals the largest number of pair-wise non-reachable vertices. Computing the width dates back to Dilworth’s and Fulkerson’s results in the 1950s, and is doable in quadratic time in the worst case. Since $k$ can be small in practical applications, research has also studied algorithms whose complexity is parameterized on $k$. Despite these efforts, it is still open whether there exists a linear-time $O(f(k)(|E| + |V|))$ parameterized algorithm computing the width. We answer this question affirmatively by presenting an $O(k2^k|E| + k^24^k|V|)$-time algorithm, based on a new notion of frontier antichains. As we process the vertices in a topological order, all the frontier antichains can be maintained with the help of several combinatorial properties, paying only $f(k)$ along the way. The fact that the width can be computed by a single $f(k)$-sweep of the DAG is a new surprising insight into this classical problem. Our algorithm also allows deciding whether the DAG has width at most $w$ in time $O(f(min(w,k))(|E|+|V|))$.
Type
Publication
In WG 2021