Chaining of Maximal Exact Matches in Graphs
Feb 5, 2023·
 ,
·
0 min read
,
·
0 min read
Nicola Rizzo
Manuel Cáceres
Veli Makinen
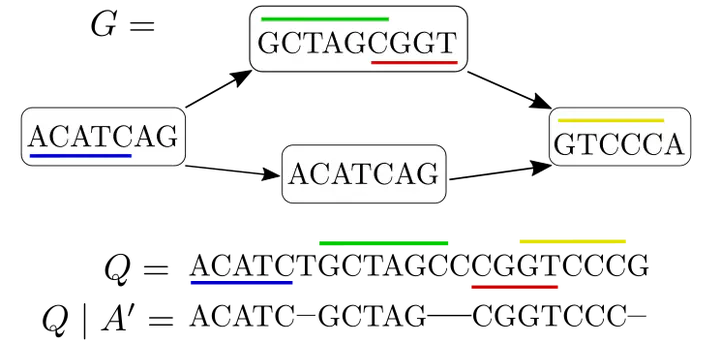 Co-linear chaining of MEMs and the corresponding induced subsequence
Co-linear chaining of MEMs and the corresponding induced subsequence
Abstract
We show how to chain maximal exact matches (MEMs) between a query string $Q$ and a labeled directed acyclic graph (DAG) $G=(V,E)$ to solve the longest common subsequence (LCS) problem between $Q$ and $G$. We obtain our result via a new symmetric formulation of chaining in DAGs that we solve in $O(m+n+k^2|V| + |E| + kN\log N)$ time, where $m=|Q|$, $n$ is the total length of node labels, $k$ is the minimum number of paths covering the nodes of $G$ and $N$ is the number of MEMs between $Q$ and node labels, which we show encode full MEMs.
Type
Publication
In SPIRE 2023