Sparsifying, Shrinking and Splicing for Minimum Path Cover in Parameterized Linear Time
Jan 9, 2022·
 ,
,
,
,
·
0 min read
,
,
,
,
·
0 min read
Manuel Cáceres
Massimo Cairo
Brendan Mumey
Romeo Rizzi
Alexandru I. Tomescu
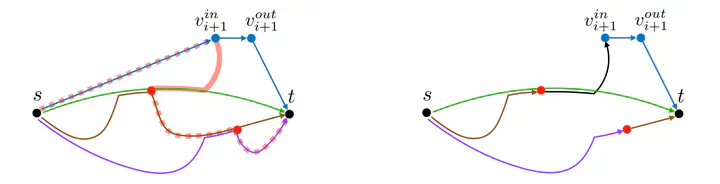 Splicing along a decrementing path
Splicing along a decrementing path
Abstract
A minimum path cover (MPC) of a directed acyclic graph (DAG) $G = (V,E)$ is a minimum-size set of paths that together cover all the vertices of the DAG. Computing an MPC is a basic polynomial problem, dating back to Dilworth’s and Fulkerson’s results in the 1950s. Since the size $k$ of an MPC (also known as the width) can be small in practical applications, research has also studied algorithms whose complexity is parameterized on $k$. We obtain two new MPC parameterized algorithms for DAGs running in time $O(k^2|V|\log(|V|) + |E|)$ and $O(k^3|V| + |E|)$. We also obtain a parallel algorithm running in $O(k^2|V| + |E|)$ parallel steps and using $O(\log(|V|))$ processors (in the PRAM model). Our latter two algorithms are the first solving the problem in parameterized linear time. Finally, we present an algorithm running in time $O(k^2|V|)$ for transforming any MPC to another MPC using less than $2|V|$ distinct edges, which we prove to be asymptotically tight. As such, we also obtain edge sparsification algorithms preserving the width of the DAG with the same running time as our MPC algorithms. At the core of all our algorithms we interleave the usage of three techniques: transitive sparsification, shrinking of a path cover, and the splicing of a set of paths along a given path.
Type
Publication
In SODA 2022