Finding Maximal Exact Matches in Graphs
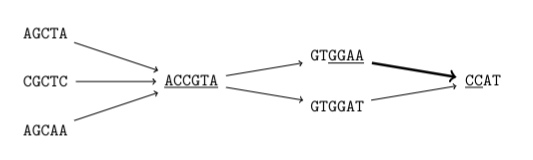 Left extension of substring ACCGTA is {A, C}, thus the substring (if also in Q) is a MEM
Left extension of substring ACCGTA is {A, C}, thus the substring (if also in Q) is a MEM
Abstract
We study the problem of finding maximal exact matches (MEMs) between a query string $Q$ and a labeled graph $G$. MEMs are an important class of seeds, often used in seed-chain-extend type of practical alignment methods because of their strong connections to classical metrics. A principled way to speed up chaining is to limit the number of MEMs by considering only MEMs of length at least $\kappa$ ($\kappa$-MEMs). However, on arbitrary input graphs, the problem of finding MEMs cannot be solved in truly sub-quadratic time under SETH (Equi et al., ICALP 2019) even on acyclic graphs. In this paper we show an $O(n\cdot L \cdot d^{L-1} + m + M_{\kappa,L})$-time algorithm finding all $\kappa$-MEMs between $Q$ and $G$ spanning exactly $L$ nodes in $G$, where $n$ is the total length of node labels, $d$ is the maximum degree of a node in $G$, $m = |Q|$, and $M_{\kappa,L}$ is the number of output MEMs. We use this algorithm to develop a $\kappa$-MEM finding solution on indexable Elastic Founder Graphs (Equi et al., Algorithmica 2022) running in time $O(nH^2 + m + M_\kappa)$, where $H$ is the maximum number of nodes in a block, and $M_\kappa$ is the total number of $\kappa$-MEMs. Our results generalize to the analysis of multiple query strings (MEMs between $G$ and any of the strings). Additionally, we provide some preliminary experimental results showing that the number of graph MEMs is orders of magnitude smaller than the number of string MEMs of the corresponding concatenated collection.