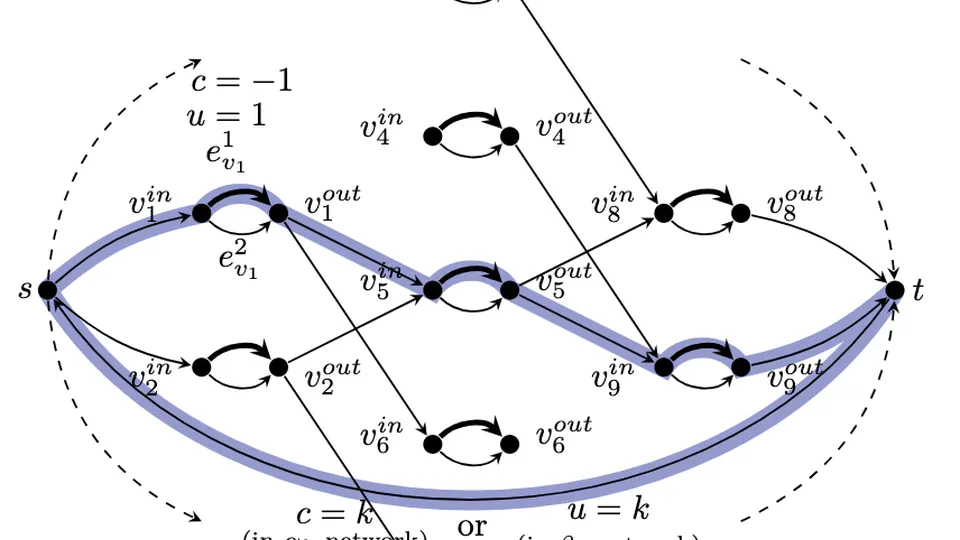
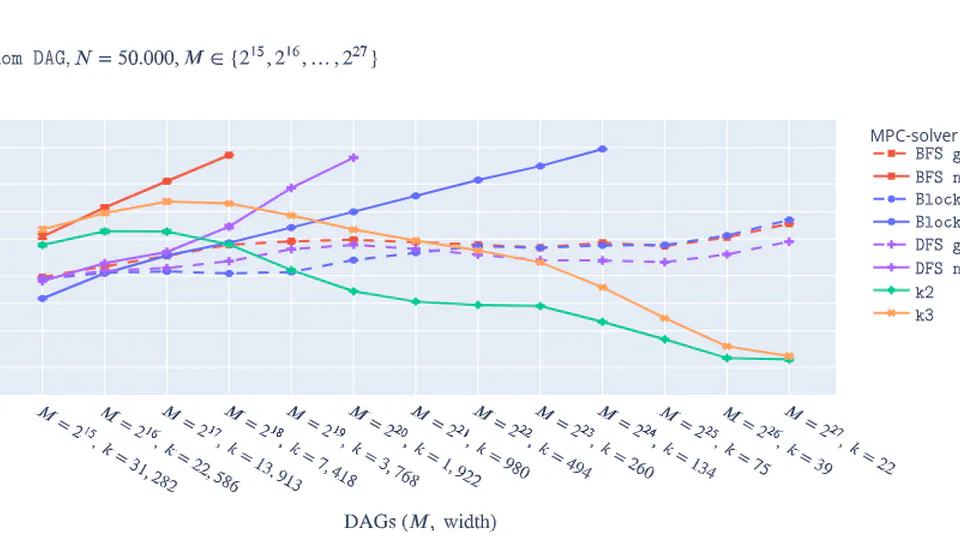
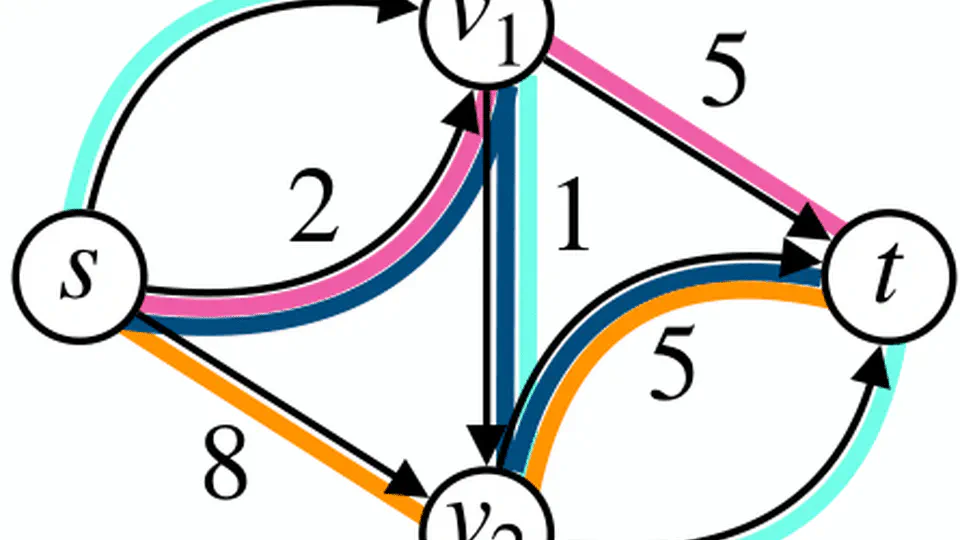
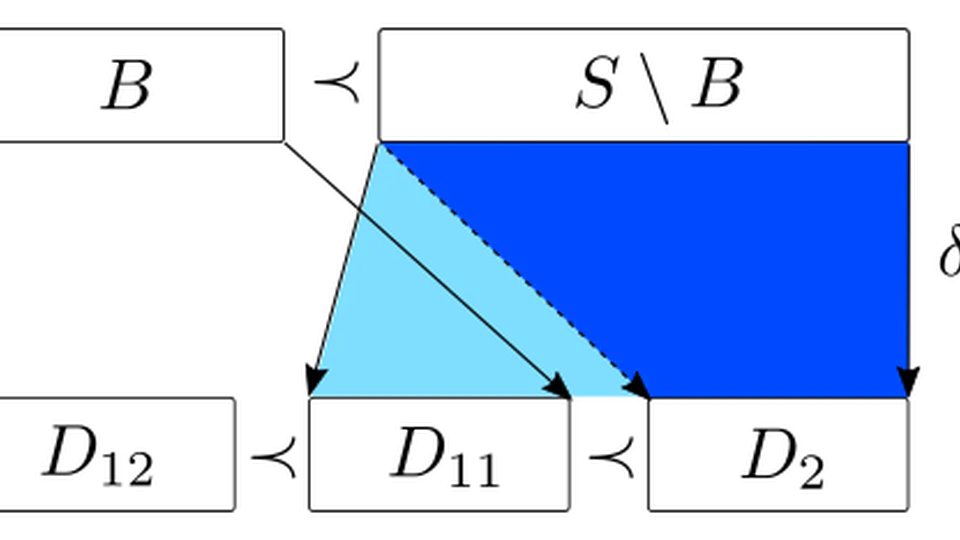
Biography

I am an HIIT Postdoctoral Fellow at Aalto University working with Professor Sándor Kisfaludi-Bak. Previously, I worked as a Postdoctoral Researcher in the group Combinatorics of Efficient Computations led by Parinya Chalermsook. Before that I was a Postdoctoral Researcher at University of Helsinki working in the Graph Algorithms team led by Alexandru I. Tomescu. Previously, I was a Doctoral Student in the same group. My Doctoral Thesis is titled “Parameterized and Safe & Complete Graph Algorithms for Bioinformatics”. Before that, I was a Master Student from the Department of Computer Science at University of Chile. I worked under the supervision of Gonzalo Navarro. My thesis is titled “Compressed Suffix Trees for Repetitive Collections based on Block Trees”.