Minimum Chain Cover in Almost Linear Time
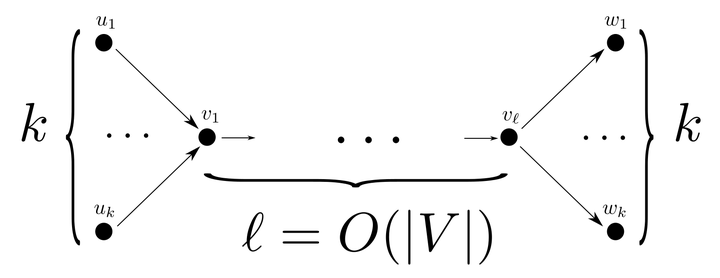 The total length of an MPC can be $\Omega(k|V|)$
The total length of an MPC can be $\Omega(k|V|)$
Abstract
A minimum chain cover (MCC) of a $k$-width directed acyclic graph (DAG) $G = (V, E)$ is a set of $k$ chains (paths in the transitive closure) of $G$ such that every vertex appears in at least one chain in the cover. The state-of-the-art solutions for MCC run in time $\tilde{O}(k(|V|+|E|))$ [Makinen et at., TALG], $O(T_{MF}(|E|) + k|V|)$, $O(k^2|V| + |E|)$ [Caceres et al., SODA 2022], $\tilde{O}(|V|^{3/2} + |E|)$ [Kogan and Parter, ICALP 2022] and $\tilde{O}(T_{MCF}(|E|) + \sqrt{k}|V|)$ [Kogan and Parter, SODA 2023], where $T_{MF}(|E|)$ and $T_{MCF}(|E|)$ are the running times for solving maximum flow (MF) and minimum-cost flow (MCF), respectively. In this work we present an algorithm running in time $O(T_{MF}(|E|) + (|V|+|E|)\log{k})$. By considering the recent result for solving MF [Chen et al., FOCS 2022] our algorithm is the first running in almost linear time. Moreover, our techniques are deterministic and derive a deterministic near-linear time algorithm for MCC if the same is provided for MF. At the core of our solution we use a modified version of the mergeable dictionaries [Farach and Thorup, Algorithmica], [Iacono and Ozkan, ICALP 2010] data structure boosted with the SIZE-SPLIT operation and answering queries in amortized logarithmic time, which can be of independent interest.