Parameterized Algorithms for String Matching to DAGs: Funnels and Beyond
Jun 26, 2023·
 ·
0 min read
·
0 min read
Manuel Cáceres
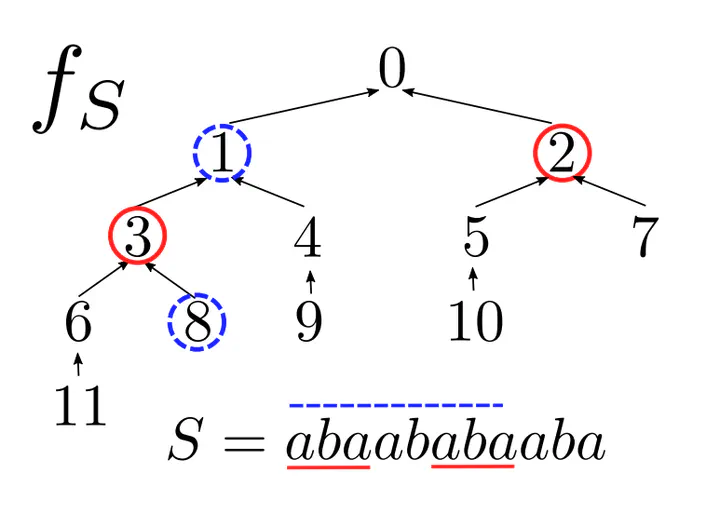 Two prefixes are incomparable iff they are not the LCA of one another in the failure tree
Two prefixes are incomparable iff they are not the LCA of one another in the failure tree
Abstract
The problem of String Matching to Labeled Graphs (SMLG) asks to find all the paths in a labeled graph $G = (V, E)$ whose spellings match that of an input string $S \in \Sigma^m$. SMLG can be solved in quadratic $O(m|E|)$ time [Amir et al., JALG], which was proven to be optimal by a recent lower bound conditioned on SETH [Equi et al., ICALP 2019]. The lower bound states that no strongly subquadratic time algorithm exists, even if restricted to directed acyclic graphs (DAGs). In this work we present the first parameterized algorithms for SMLG in DAGs. Our parameters capture the topological structure of $G$. All our results are derived from a generalization of the Knuth-Morris-Pratt algorithm [Park and Kim, CPM 1995] optimized to work in time proportional to the number of prefix-incomparable matches. To obtain the parameterization in the topological structure of $G$, we first study a special class of DAGs called funnels [Millani et al., JCO] and generalize them to $k$-funnels and the class $ST_k$. We present several novel characterizations and algorithmic contributions on both funnels and their generalizations.
Type
Publication
Best paper in CPM 2023