Safety and Completeness in Flow Decompositions for RNA Assembly
May 9, 2022·
,
 ,
,
·
0 min read
,
,
·
0 min read
Shahbaz Khan
Milla Kortelainen
Manuel Cáceres
Lucia Williams
Alexandru I. Tomescu
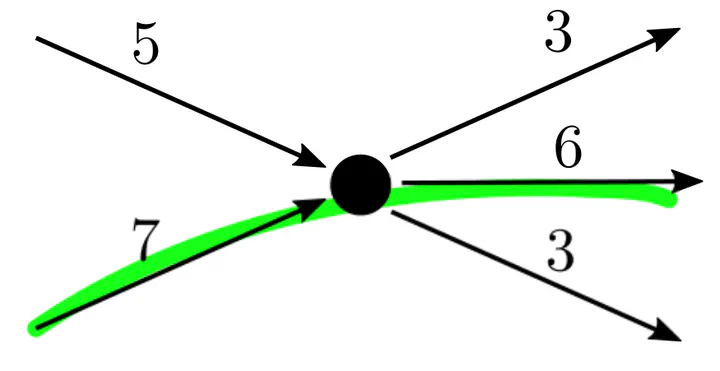 Safe flow subpath, which is not an extended unitig
Safe flow subpath, which is not an extended unitig
Abstract
Decomposing a network flow into weighted paths is a problem with numerous applications, ranging from networking, transportation planning to bioinformatics. In some applications we look for any decomposition that is optimal with respect to some property, such as number of paths used, robustness to edge deletion, or length of the longest path. However, in many bioinformatic applications, we seek a specific decomposition where the paths correspond to some underlying data that generated the flow. For realistic inputs, no optimization criteria can be guaranteed to uniquely identify the correct decomposition. Therefore, we propose to instead report the {m safe} paths, which are subpaths of at least one path in every flow decomposition.
Recently, Ma, Zheng, and Kingsford [WABI 2020] addressed the existence of multiple optimal solutions in a probabilistic framework, which is referred to as non-identifiability. In a follow-up work [RECOMB 2021], they gave a quadratic-time algorithm based on a global criterion for solving a problem called AND-Quant, which generalizes the problem of reporting whether a given path is safe.
In this work, we give the first local characterization of safe paths for flow decompositions in directed acyclic graphs (DAGs), leading to a practical algorithm for finding the complete set of safe paths. We additionally evaluated our algorithm against the trivial safe algorithms (unitigs, extended unitigs) and the popularly used heuristic (greedy-width) for flow decomposition on RNA transcripts datasets. We find that despite maintaining perfect precision the safe and complete algorithm reports significantly higher coverage (~50% more) as compared to trivial safe algorithms. The greedy-width algorithm though reporting a better coverage, reports significantly lower precision on complex graphs (for genes expressing a large number of transcripts). Overall, our safe and complete algorithm outperforms (by ~20%) greedy-width on a unified metric (F-Score) considering both coverage and precision when the evaluated dataset has significant number of complex graphs. Moreover, it also has superior time (3-5x) and space efficiency (1.2-2.2x), resulting in a better and more practical approach for bioinformatics applications of flow decomposition.
Type
Publication
In RECOMB 2022