Practical Minimum Path Cover
Jun 1, 2024·
 ,
,
,
·
0 min read
,
,
,
·
0 min read
Manuel Cáceres
Brendan Mumey
Santeri Toivonen
Alexandru I. Tomescu
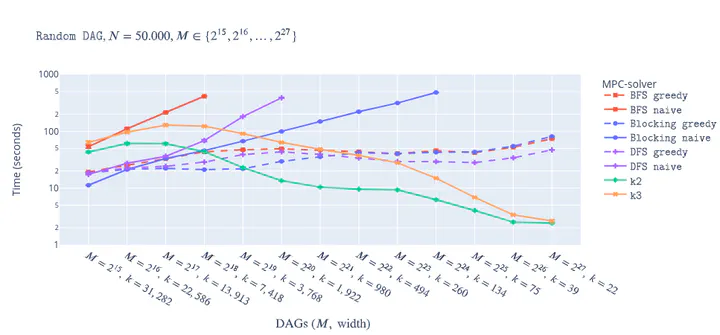 Running time (log scale) of random DAG for different densities and algorithms
Running time (log scale) of random DAG for different densities and algorithms
Abstract
Computing a minimum path cover (MPC) of a directed acyclic graph (DAG) is a fundamental problem with a myriad of applications, including reachability. Although it is known how to solve the problem by a simple reduction to minimum flow, recent theoretical advances exploit this idea to obtain algorithms parameterized by the number of paths of an MPC, known as the width. These results obtain fast [Mäkinen et al., TALG] and even linear time [Cáceres et al., SODA 2022] algorithms in the small-width regime. In this paper, we present the first publicly available high-performance implementation of state-of-the-art MPC algorithms, including the parameterized approaches. Our experiments on random DAGs show that parameterized algorithms are orders-of-magnitude faster on dense graphs. Additionally, we present new pre-processing heuristics based on transitive edge sparsification. We show that our heuristics improve MPC-solvers by orders-of-magnitude.
Type
Publication
In SEA 2024