Practical colinear chaining on sequences revisited
Jun 8, 2025·
 ,
·
0 min read
,
·
0 min read
Nicola Rizzo
Manuel Cáceres
Veli Mäkinen
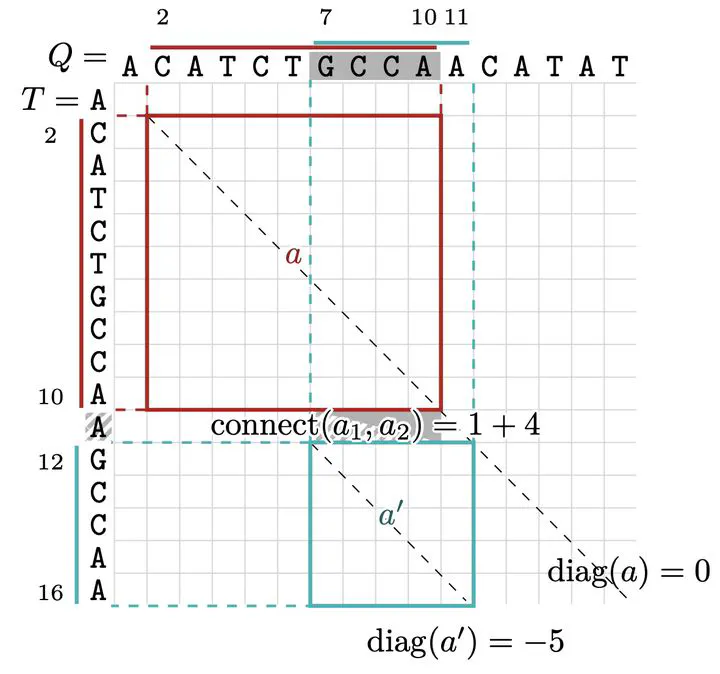 Diagonal distance between anchors
Diagonal distance between anchors
Abstract
Colinear chaining is a classical heuristic for sequence alignment and is widely used in modern practical aligners. Jain et al. (J. Comput. Biol. 2022) proposed an $O(n\log_{3}n)$ time algorithm to chain a set of n anchors so that the chaining cost matches the edit distance of the input sequences, when anchors are all the maximal exact matches. Moreover, assuming a uniform and sparse distribution of anchors, they provided a practical solution ($\texttt{Chainx}$) working in $O(n\cdot SOL+n\log n)$ average-case time, where $SOL$ is the cost of the output chain. This practical solution is not guaranteed to be optimal: we study the failing cases, introduce the anchor diagonal distance, and find and implement an optimal algorithm working in $O(n\cdot OPT+n\log n)$ average-case time, where OPT $\le SOL$ is the optimal chaining cost. We validate the results by Jain et al., show that $\texttt{ChainX}$ can be suboptimal with a realistic long read dataset, and show minimal computational slowdown for our solution.
Type
Publication
In ISBRA 2025