Width Helps and Hinders Splitting Flows
Sep 9, 2022·
 ,
,
,
,
,
,
,
·
0 min read
,
,
,
,
,
,
,
·
0 min read
Manuel Cáceres
Massimo Cairo
Andreas Grigorjew
Shahbaz Khan
Brendan Mumey
Romeo Rizzi
Alexandru I. Tomescu
Lucia Williams
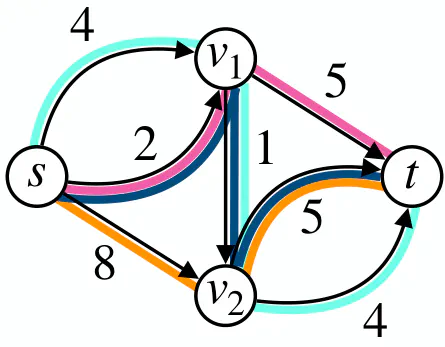 Flow decomposition using negative weights can yield to a smaller solution
Flow decomposition using negative weights can yield to a smaller solution
Abstract
Minimum flow decomposition (MFD) is the NP-hard problem of finding a smallest decomposition of a network flow $X$ on directed graph $G$ into weighted source-to-sink paths whose superposition equals $X$. We focus on a common formulation of the problem where the path weights must be non-negative integers and also on a new variant where these weights can be negative. We show that, for acyclic graphs, considering the width of the graph (the minimum number of $s$-$t$ paths needed to cover all of its edges) yields advances in our understanding of its approximability. For the non-negative version, we show that a popular heuristic is a $O( \log |X|)$-approximation ($|X|$ being the total flow of $X$) on graphs satisfying two properties related to the width (satisfied by e.g., series-parallel graphs), and strengthen its worst-case approximation ratio from $\Omega(\sqrt{m})$ to $\Omega(m / \log m)$ for sparse graphs, where $m$ is the number of edges in the graph. For the negative version, we give a $(\lceil \log \Vert X \Vert \rceil +1)$-approximation ($\Vert X \Vert$ being the maximum absolute value of $X$ on any edge) using a power-of-two approach, combined with parity fixing arguments and a decomposition of unitary flows ($\Vert X \Vert \leq 1$) into at most width paths. We also disprove a conjecture about the linear independence of minimum (non-negative) flow decompositions posed by Kloster et al. [ALENEX 2018], but show that its useful implication (polynomial-time assignments of weights to a given set of paths to decompose a flow) holds for the negative version.
Type
Publication
In ESA 2022