Conference-Paper

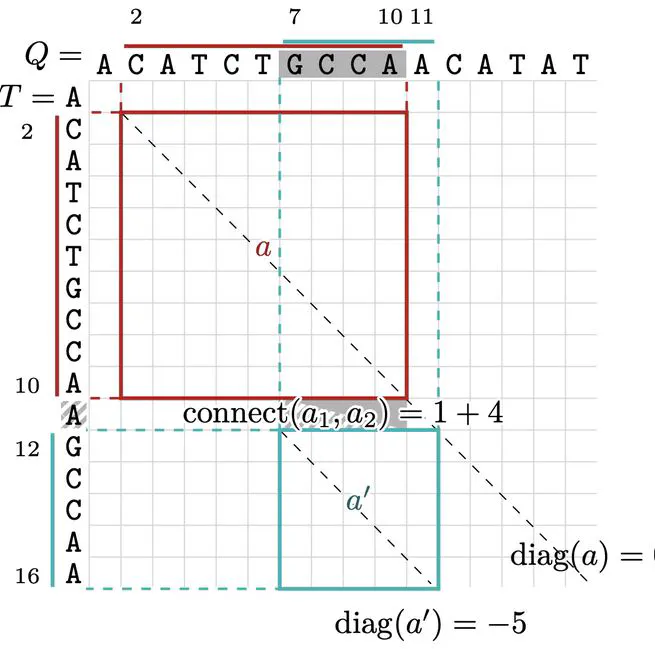
We study the failing cases of $\texttt{Chainx}$, introduce the anchor diagonal distance, and find and implement an optimal algorithm working in $O(n\cdot OPT+n\log n)$ average-case time, where OPT $\le SOL$ is the optimal chaining cost.

Jun 8, 2025

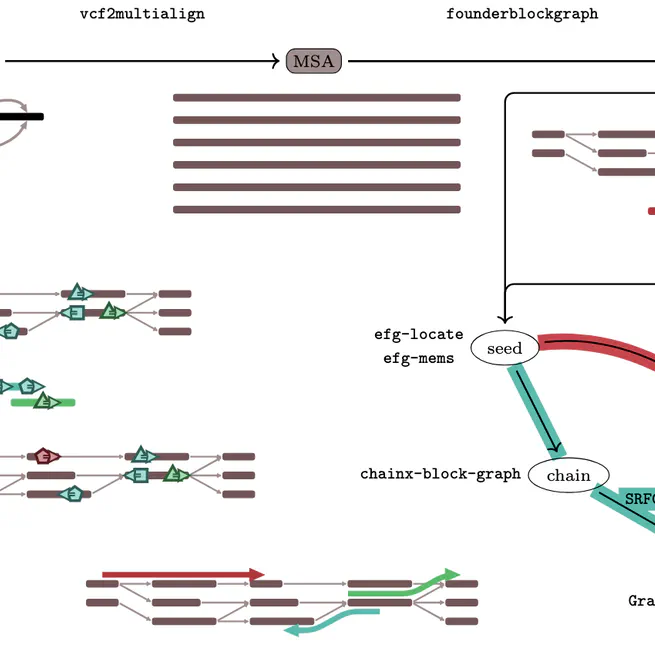
We implement a complete seed-chain-extend alignment workflow based on indexable elastic founder graphs (iEFGs). We show how to construct iEFGs from the variations to a linear reference, find high-quality seeds, and extend them using GraphAligner, at the scale of a telomere-to-telomere assembled human chromosome.

Apr 8, 2025

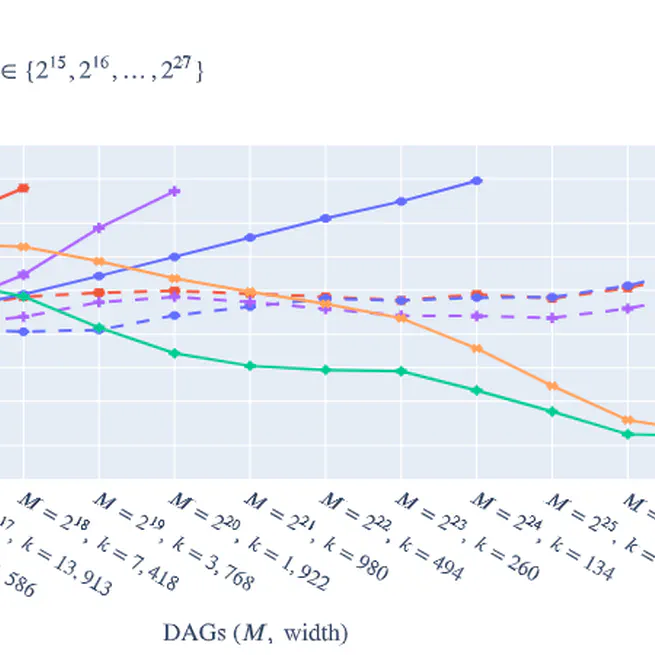
We present the first publicly available high-performance implementation of state-of-the-art MPC algorithms, including the parameterized approaches. Our experiments on random DAGs show that parameterized algorithms are orders-of-magnitude faster on dense graphs. Additionally, we present new pre-processing heuristics based on transitive edge sparsification. We show that our heuristics improve MPC-solvers by orders-of-magnitude.

Jun 1, 2024

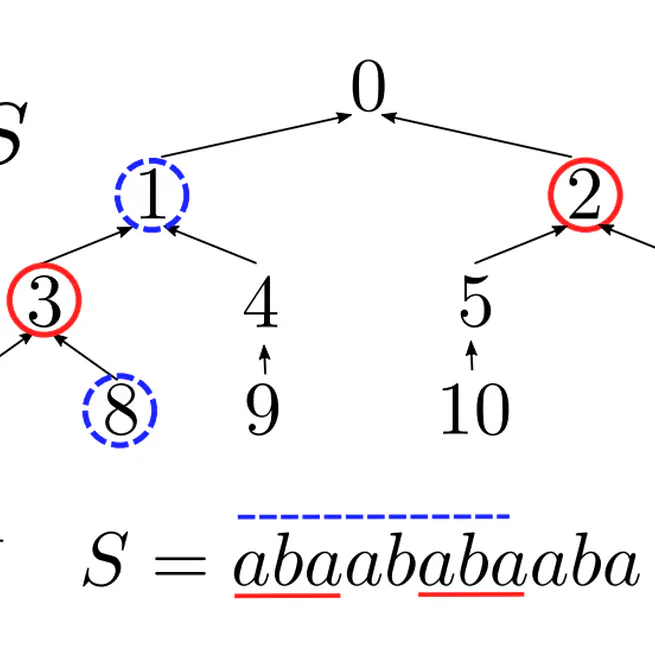
We present the first parameterized algorithms for SMLG in DAGs, derived from a generalization of the Knuth-Morris-Pratt algorithm optimized to work in time proportional to the number of prefix-incomparable matches. We obtain parameterizations in the topological structure of $G$, by studying a special class of DAGs called funnels and generalizing them to $k$-funnels and the class $ST_k$.

Jun 26, 2023

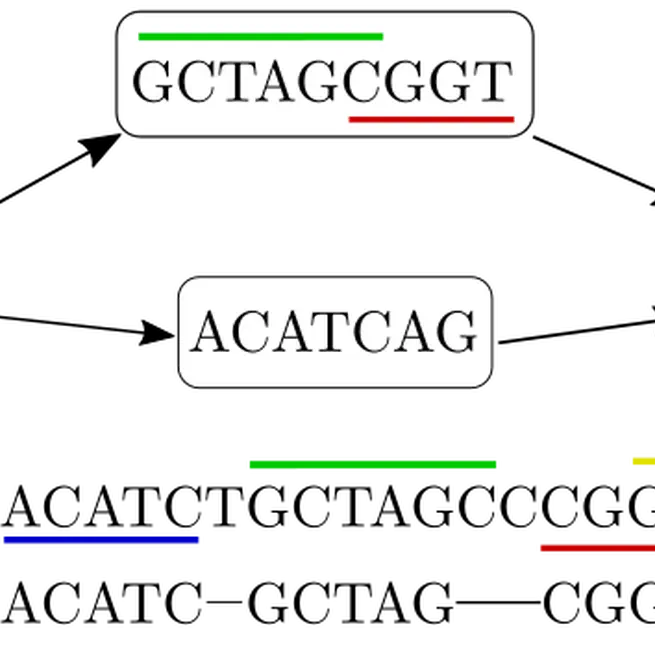
We show an $O(n\cdot L \cdot d^{L-1} + m + M_{\kappa,L})$-time algorithm finding all $\kappa$-MEMs between $Q$ and $G$ spanning exactly $L$ nodes in $G$, where $n$ is the total length of node labels, $d$ is the maximum degree of a node in $G$, $m = |Q|$, and $M_{\kappa,L}$ is the number of output MEMs.

Feb 5, 2023

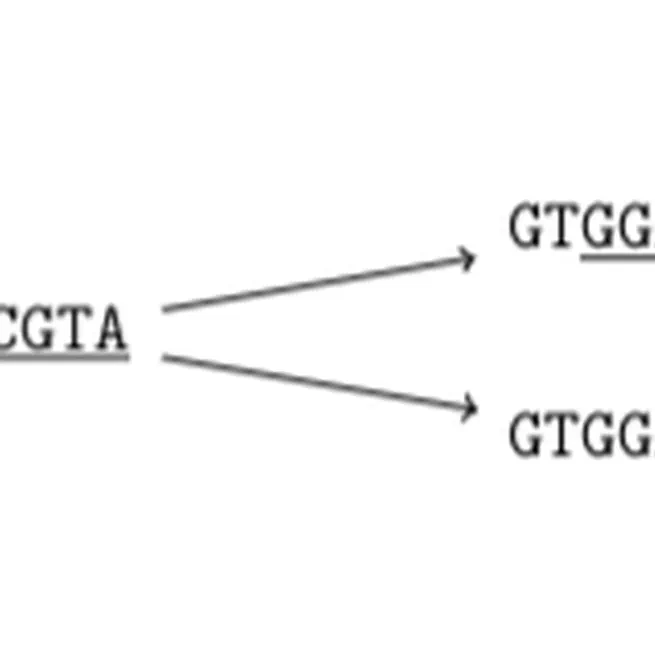
We show how to chain *maximal exact matches* (MEMs) between a query string $Q$ and a labeled directed acyclic graph (DAG) $G=(V,E)$ to solve the *longest common subsequence* (LCS) problem between $Q$ and $G$.

Feb 5, 2023

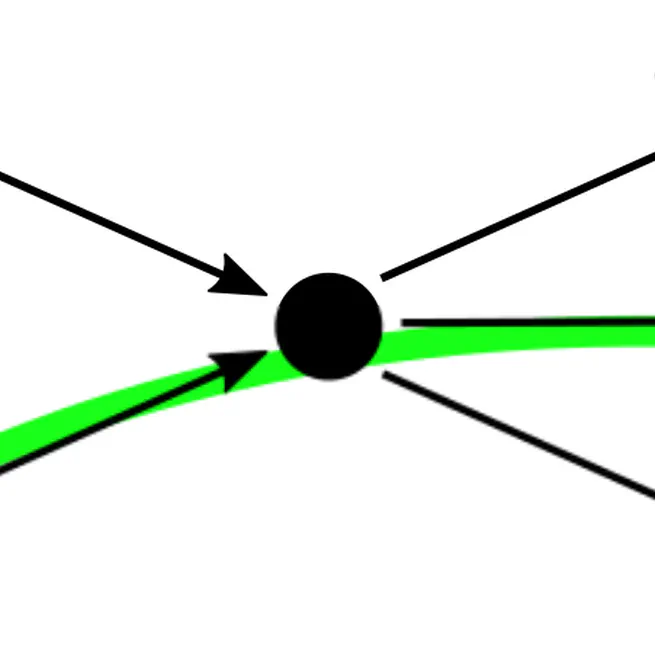
We give the first local characterization of safe paths for flow decompositions in directed acyclic graphs (DAGs), leading to a practical algorithm for finding the complete set of safe paths. We additionally evaluated our algorithms against the trivial safe algorithms (unitigs, extended unitigs) and the popularly used heuristic (greedy-width) for flow decomposition on RNA transcripts datasets. We find that despite maintaining perfect precision the safe and complete algorithm reports significantly higher coverage as compared to trivial safe algorithms.

May 9, 2022

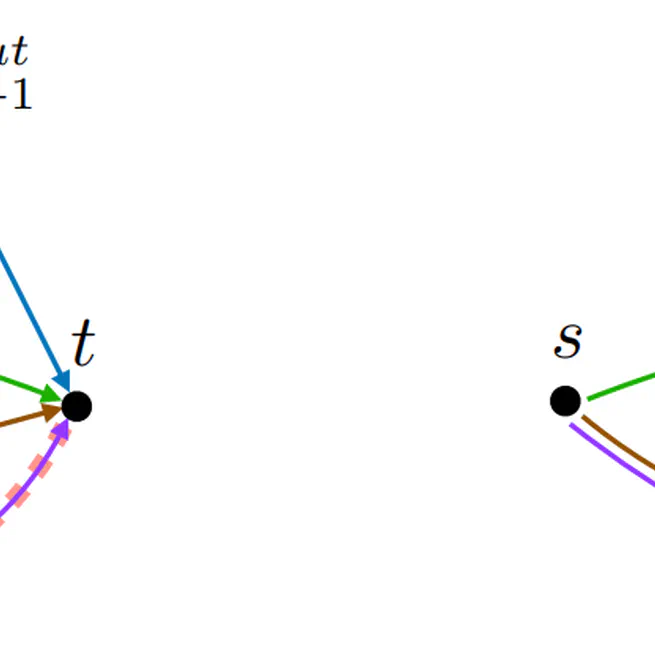
We obtain two new MPC parameterized algorithms for DAGs running in time $O(k^2|V|\log(|V|) + |E|)$ and $O(k^3|V| + |E|)$. We also obtain a parallel algorithm running in $O(k^2|V| + |E|)$ parallel steps and using $O(\log(|V|))$ processors (in the PRAM model). We also obtain edge sparsification algorithms preserving the width of the DAG with the same running time as our MPC algorithms.

Jan 9, 2022

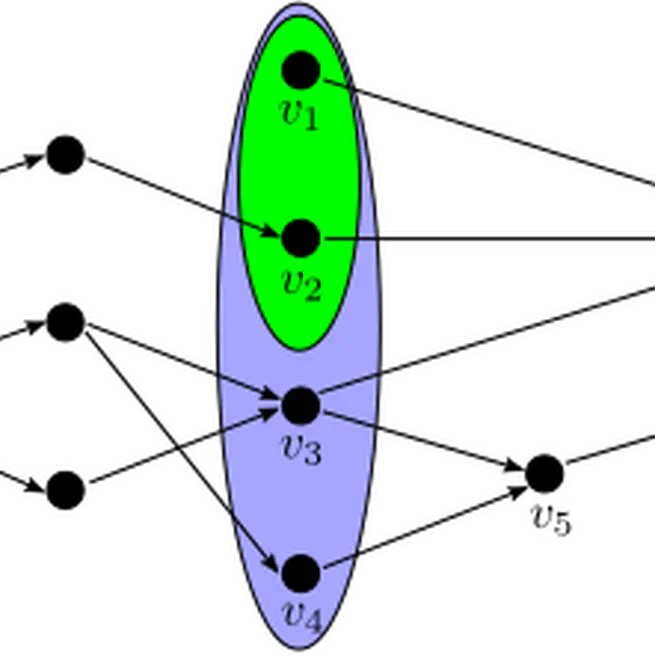
We describe an parameterized algorithm to compute the width $k$ of a DAG in time $O(k2^k|E| + k^24^k|V|)$.

Aug 1, 2021

We describe indexes for searching large data sets for variable-length-gapped (VLG) patterns. Our best approach provides search speeds several times faster than prior art across a broad range of patterns and texts.

Jan 17, 2020