Conference Publication

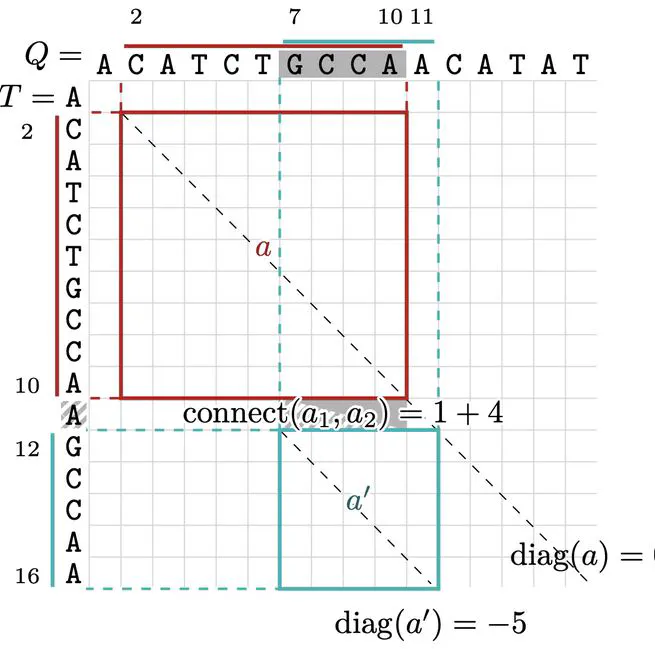
We study the failing cases of $\texttt{Chainx}$, introduce the anchor diagonal distance, and find and implement an optimal algorithm working in $O(n\cdot OPT+n\log n)$ average-case time, where OPT $\le SOL$ is the optimal chaining cost.

Jun 8, 2025

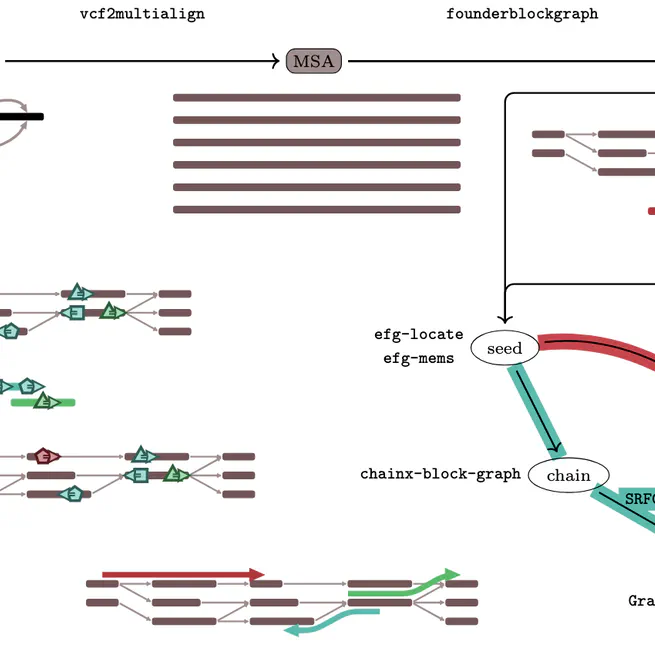
We implement a complete seed-chain-extend alignment workflow based on indexable elastic founder graphs (iEFGs). We show how to construct iEFGs from the variations to a linear reference, find high-quality seeds, and extend them using GraphAligner, at the scale of a telomere-to-telomere assembled human chromosome.

Apr 8, 2025

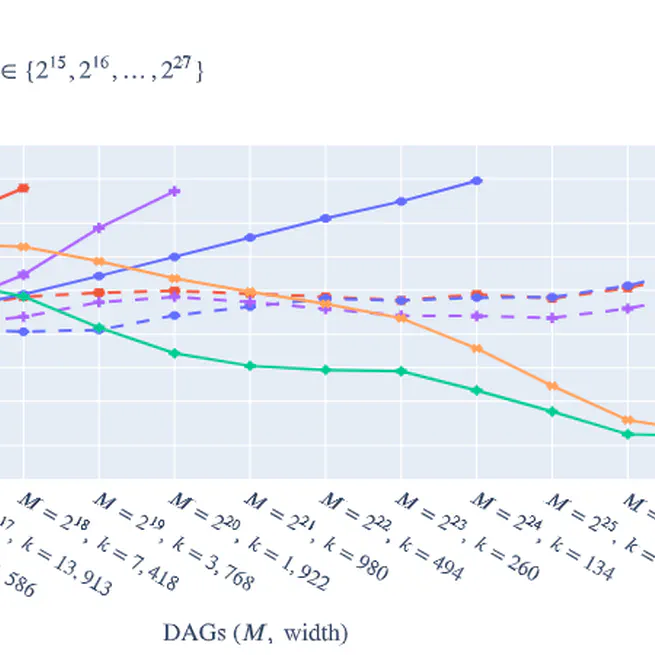
We present the first publicly available high-performance implementation of state-of-the-art MPC algorithms, including the parameterized approaches. Our experiments on random DAGs show that parameterized algorithms are orders-of-magnitude faster on dense graphs. Additionally, we present new pre-processing heuristics based on transitive edge sparsification. We show that our heuristics improve MPC-solvers by orders-of-magnitude.

Jun 1, 2024

We provide a $O(|\delta| \log |Q|)$-time algorithm computing a co-lex total preorder when the input is a Wheeler NFA, and an algorithm with the same time complexity computing the smallest-width co-lex partial order of any DFA.

Sep 4, 2023

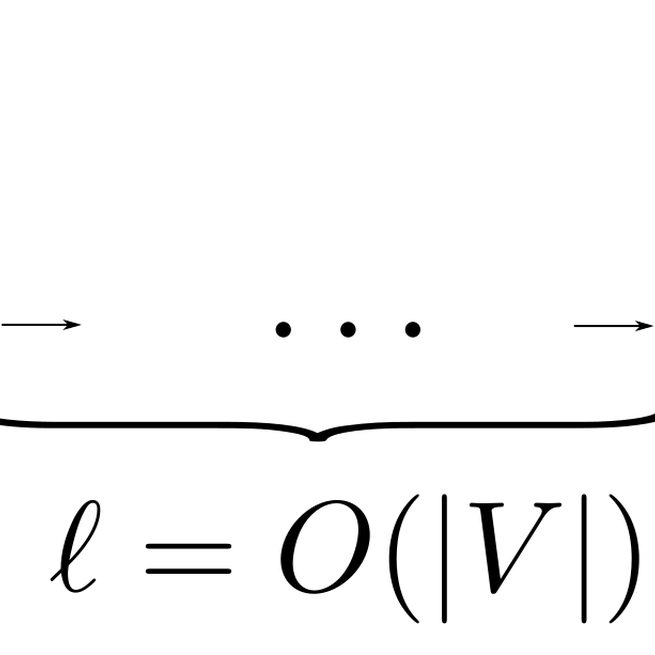
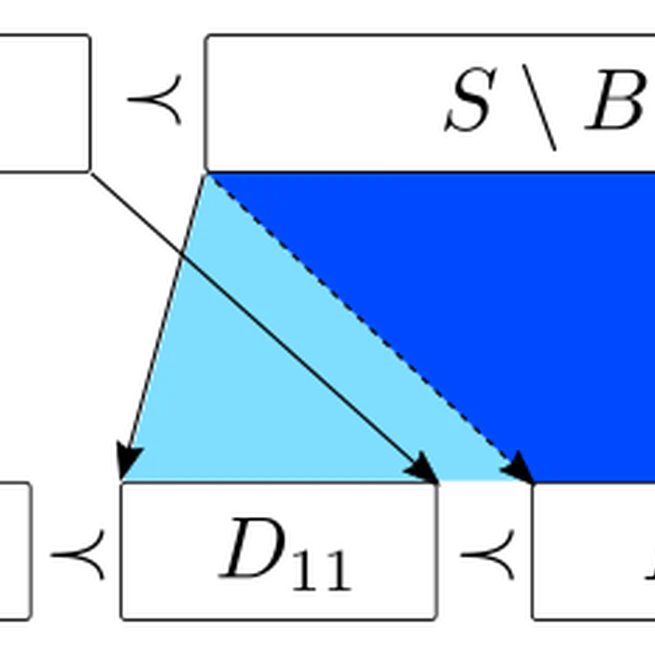
A minimum chain cover (MCC) of a $k$-width directed acyclic graph (DAG) $G = (V, E)$ is a set of $k$ chains (paths in the transitive closure) of $G$ such that every vertex appears in at least one chain in the cover. We present an algorithm running in time $O(T_{MF}(|E|) + (|V|+|E|)\log{k})$.

Jul 10, 2023

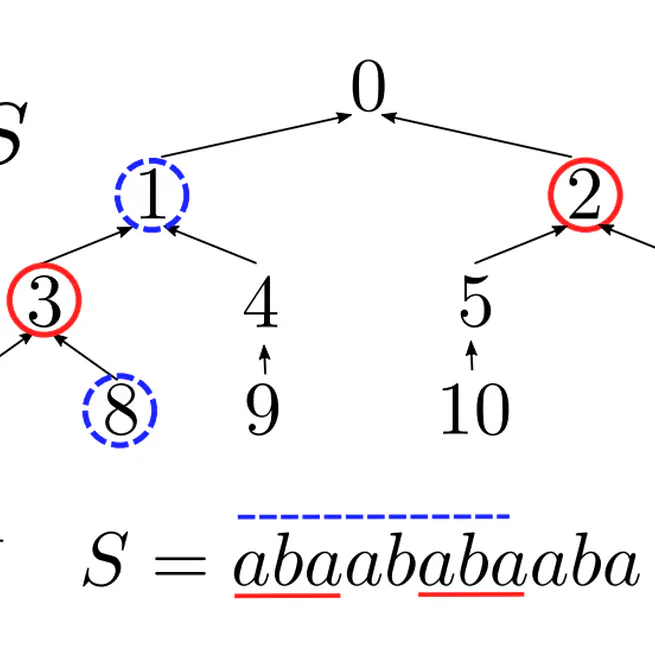
We present the first parameterized algorithms for SMLG in DAGs, derived from a generalization of the Knuth-Morris-Pratt algorithm optimized to work in time proportional to the number of prefix-incomparable matches. We obtain parameterizations in the topological structure of $G$, by studying a special class of DAGs called funnels and generalizing them to $k$-funnels and the class $ST_k$.

Jun 26, 2023

We show an $O(n\cdot L \cdot d^{L-1} + m + M_{\kappa,L})$-time algorithm finding all $\kappa$-MEMs between $Q$ and $G$ spanning exactly $L$ nodes in $G$, where $n$ is the total length of node labels, $d$ is the maximum degree of a node in $G$, $m = |Q|$, and $M_{\kappa,L}$ is the number of output MEMs.

Feb 5, 2023

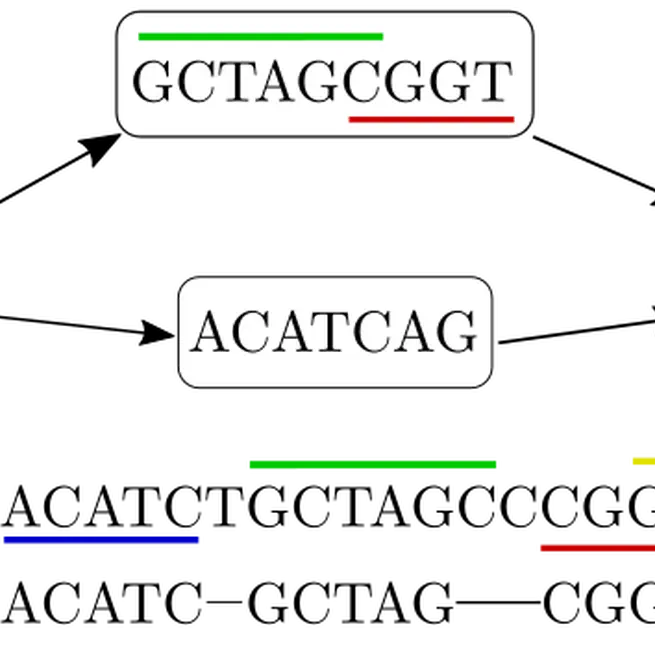
We show how to chain *maximal exact matches* (MEMs) between a query string $Q$ and a labeled directed acyclic graph (DAG) $G=(V,E)$ to solve the *longest common subsequence* (LCS) problem between $Q$ and $G$.

Feb 5, 2023

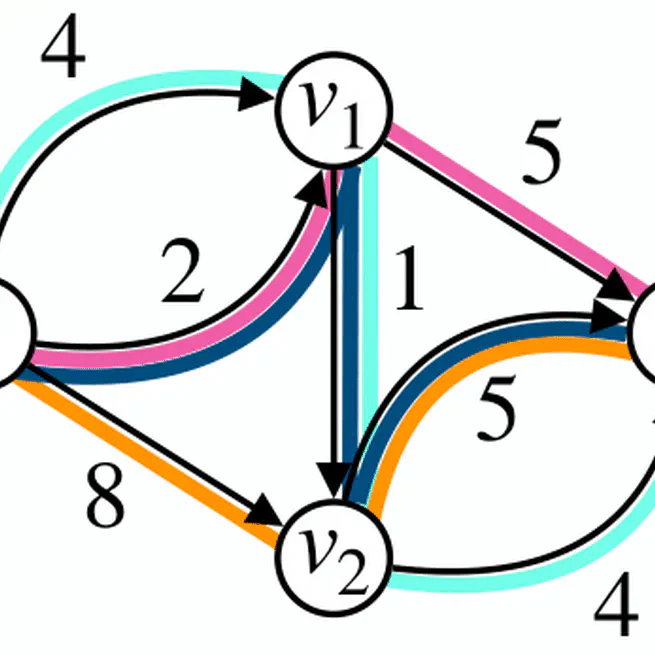
We show that, for acyclic graphs, considering the width of the graph yields advances in our understanding of its approximability. For the non-negative version, we show that a popular heuristic is a $O( \log |X|)$-approximation on graphs satisfying two properties related to the width (satisfied by e.g., series-parallel graphs), and strengthen its worst-case approximation ratio for sparse graphs. For the negative version, we give a $(\lceil \log \Vert X \Vert \rceil +1)$-approximation using a power-of-two approach, combined with parity fixing arguments and a decomposition of unitary flows ($\Vert X \Vert \leq 1$) into at most width paths.

Sep 9, 2022

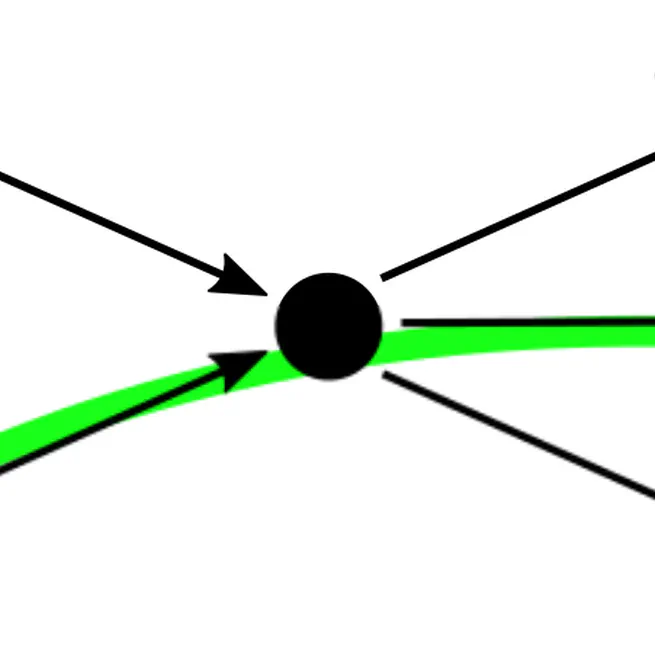
We give the first local characterization of safe paths for flow decompositions in directed acyclic graphs (DAGs), leading to a practical algorithm for finding the complete set of safe paths. We additionally evaluated our algorithms against the trivial safe algorithms (unitigs, extended unitigs) and the popularly used heuristic (greedy-width) for flow decomposition on RNA transcripts datasets. We find that despite maintaining perfect precision the safe and complete algorithm reports significantly higher coverage as compared to trivial safe algorithms.

May 9, 2022