A Safety Framework for Flow Decomposition Problems via Integer Linear Programming
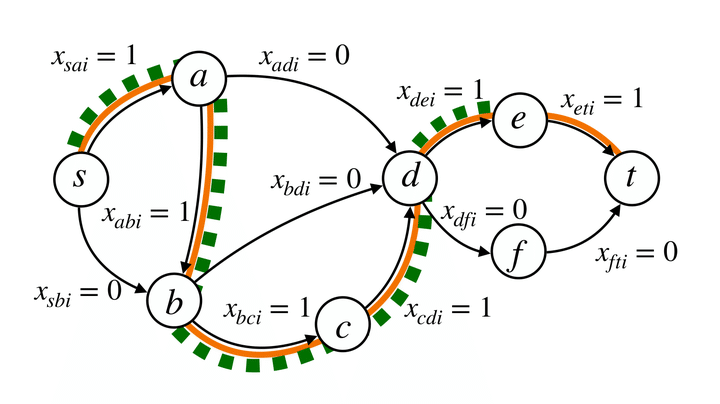 Path safety test encoded as ILP
Path safety test encoded as ILP
Abstract
Many important problems in Bioinformatics (e.g., assembly or multi-assembly) admit multiple solutions, while the final objective is to report only one. A common approach to deal with this uncertainty is finding safe partial solutions (e.g., contigs) which are common to all solutions. Previous research on safety has focused on polynomially-time solvable problems, whereas many successful and natural models are NP-hard to solve, leaving a lack of safety tools for such problems. We propose the first method for computing all safe solutions for an NP-hard problem, minimum flow decomposition. We obtain our results by developing a safety test for paths based on a general Integer Linear Programming (ILP) formulation. Moreover, we provide implementations with practical optimizations aimed to reduce the total ILP time, the most efficient of these being based on a recursive group-testing procedure. Experimental results on the transcriptome datasets of Shao and Kingsford (TCBB, 2017) show that all safe paths for minimum flow decompositions correctly recover up to 90% of the full RNA transcripts, which is at least 25% more than previously known safe paths, such as (Caceres et al. TCBB, 2021), (Zheng et al., RECOMB 2021), (Khan et al., RECOMB 2022, ESA 2022). Moreover, despite the NP-hardness of the problem, we can report all safe paths for 99.8% of the over 27,000 non-trivial graphs of this dataset in only 1.5 hours. Our results suggest that, on perfect data, there is less ambiguity than thought in the notoriously hard RNA assembly problem